What is TLA+?

A language for high-level modeling of digital systems.

TLA+ Tools

• TLA Toolbox (IDE).
• TLC model checker.
• TLAPS: TLA+ Proof System.

A language for high-level modeling of digital systems.

• At the design level.
• Above the code level.

A language for high-level modeling of digital systems.

• Abstraction.
• Avoid non critical parts.
• Avoid lower-level implementation details.

A language for high-level modeling of digital systems.

• Algorithms.
• Protocols (2PC, Paxos).
• Programs: specially complex concurrent/distributed programs.

Benefits

• Can help find and detect design errors.
• Before writing any code.
• Some errors are very hard to detect by testing: concurrent/distributed systems.
• Provides a new way of thinking about the system (a scientific approach).
• Let us understand complex systems.
• Level up your abstraction skills (better programmers?).

Getting Started with TLA+

• How can we think more clearly? Thinking like a scientist.
• Science makes mathematical models of reality.
• TLA+ uses simple maths: more expressive and simpler than a programming language.

Standard Behavioral Model

• A program execution is represented by a behavior.
• A program is modeled by a set of behaviors.
• A behavior is a sequence of states.
• A state is an assignment of values to variables.

A Simple Example

int i ;
void main()
    { i = someNumber () ;
      i = i + 1 ;
    }		
	    

A Simple Example

• Posible initial values of variables.
• The relation between the values in the current state and their possible values in the next state.

A Simple Example: The Spec (pretty printed)

A Simple Example: The Spec (in ASCII)

--------------------------- MODULE SimpleProgram ---------------------------

EXTENDS Integers
VARIABLES i, pc

Init == (pc = "start") /\ (i = 0)

Pick == \/ /\ pc = "start"
           /\ i' \in 0..1000
           /\ pc' = "middle"

Add1 == \/ /\ pc = "middle"
           /\ i' = i + 1
           /\ pc' = "done"

Next == \/ Pick 
        \/ Add1

=============================================================================		
	    

Exercise 1

Write the TLA+ specification to compute the GCD with the Euclid's algorithm.

Computes GCD of M and N by:

• Initialize x to M and y to N.
• Keep substracting the smaller of x and y from the larger.
• Stop when x = y.

Check your solution with TLC model checker to compute the GCD of inputs.

Solution to Exercise 1 (pretty printed)

Solution to Exercise 1 (in ASCII)

------------------------------- MODULE Euclid -------------------------------

EXTENDS Integers

CONSTANTS M, N
VARIABLES x, y

Init == (x = M) /\ (y = N)

Next == \/ /\ x < y
           /\ y' = y - x
           /\ x' = x
        \/ /\ y < x
           /\ x' = x-y
           /\ y' = y

Spec == Init /\ [][Next]_<>

=============================================================================
	    

Exercise 2

Water Jug problem of Die Hard 3

Solution Exercise 2 (in ASCII)

------------------------------ MODULE DieHard ------------------------------

EXTENDS Naturals

VARIABLES big,   \* The number of gallons of water in the 5 gallon jug.
          small  \* The number of gallons of water in the 3 gallon jug.


TypeOK == /\ small \in 0..3 
          /\ big   \in 0..5


Init == /\ big = 0 
        /\ small = 0

FillSmallJug  == /\ small' = 3 
                 /\ big' = big

FillBigJug    == /\ big' = 5 
                 /\ small' = small

EmptySmallJug == /\ small' = 0 
                 /\ big' = big

EmptyBigJug   == /\ big' = 0 
                 /\ small' = small

Min(m,n) == IF m < n THEN m ELSE n

SmallToBig == /\ big'   = Min(big + small, 5)
              /\ small' = small - (big' - big)

BigToSmall == /\ small' = Min(big + small, 3) 
              /\ big'   = big - (small' - small)

Next ==  \/ FillSmallJug 
         \/ FillBigJug    
         \/ EmptySmallJug 
         \/ EmptyBigJug    
         \/ SmallToBig    
         \/ BigToSmall    

Spec == Init /\ [][Next]_<> 

=============================================================================
	    

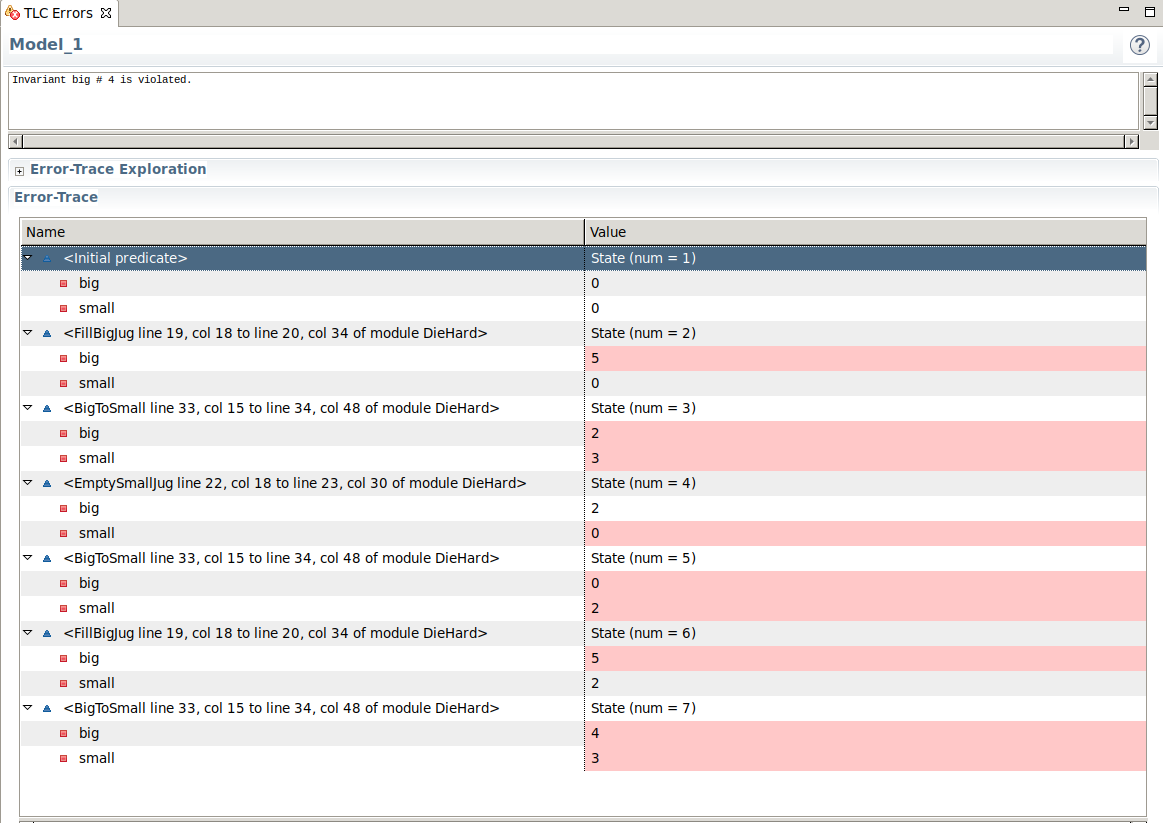
Use TLC Model Checker to find the problem solution

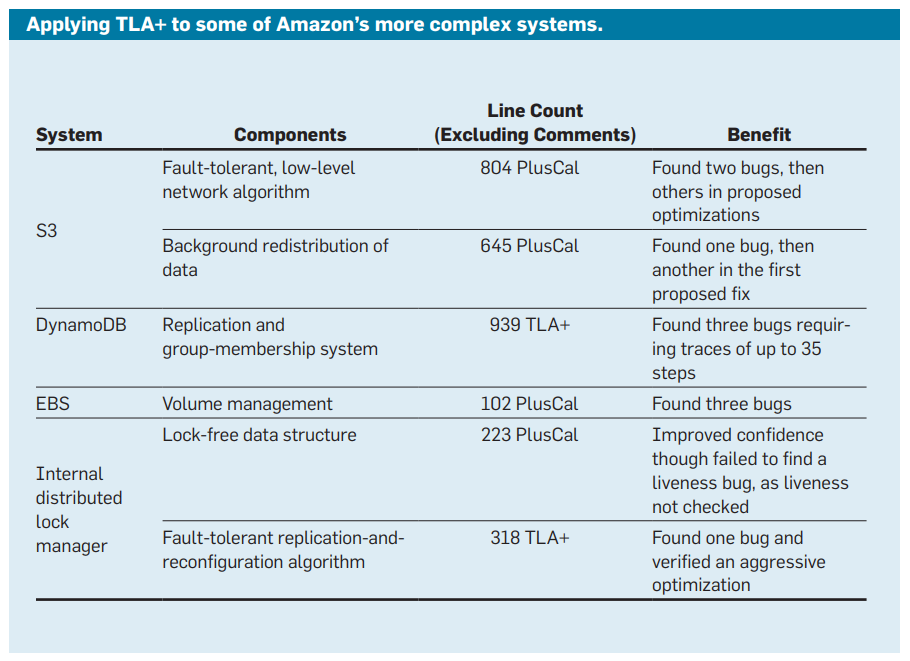
How Amazon Web Services Uses Formal Methods

“Formal methods find bugs in system designs that cannot be found through any other technique we know of.”

“At Amazon, formal methods are routinely applied to the design of complex real-world software, including public cloud services.”

“A precise, testable description of a system becomes a whatif tool for designs, analogous to how spreadsheets are a what-if tool for financial models.”

“Executive management actively encourages teams to write TLA+ specs for new features and other significant design changes.”

Debugging a Concurrent Java Program

References

• Specifying Systems by Leslie Lamport.
• Practical TLA+ by Hillel Wayne.
• Learn TLA
• How Amazon Web Services Uses Formal Methods